之前有同学问我,怎么在一个集合中高效的找到最大以及最小的元素?(注意,不是总是找最大元素,或者总是找最小元素,而是类似随机的查找最大以及最小元素。)一开始有几种想法:
朴素的想法
把集合遍历一遍,就可以知道最大或者最小元素了,查找复杂度是O(N),查找并删除的复杂度也是O(N)。
堆结构
用两个堆,一个最大堆,一个最小堆,两个堆各存一份数据。查找最大元素,就在最大堆里面找;查找最小元素,就在最小堆里面找,他们的查找时间复杂度是O(1),查找并删除的复杂度是O(logN)。但是,怎么“同步”这两个堆呢?即,在最大堆里面删除最小的元素,在最小堆里面删除最大的元素。我们知道的只是:最小(大)元素在最大(小)堆的叶子上。怎么判断节点是叶子呢?下标×2 > size就是叶子,但是叶子上面的元素又不是排序的,查找的复杂度只能是O(N)。所以,这种想法的复杂度还是O(N)。
双端堆(灯,等灯等灯!)
突然想到小倩同学之前好像说过一个叫双端堆的数据结构,可以同时高效的查找最大最小元素。问了下小倩,然后又发现原来最近看的《数据结构基础》上面,就有相关的内容,只不过里面不叫双端堆,而是叫做对称最小-最大堆。(我个人感觉这两种名称讲的就是同一个数据结构)它就可以在O(1)的复杂度的情况下,找到最小(大)元素;O(logN)的情况下找到并删除最小(大)元素。
双端堆的特点
双端堆是一棵满二叉树,最顶端的根是一个虚根,不存放数据。定义element(N)为节点N的所有子孙节点(不包括N本身)的集合,N的左孩子left(N)(如果有的话)是element(N)中最小的元素,右孩子right(N)(如果有的话)是element(N)中最大的元素。
当以下条件成立时,它才是双端堆:
P1:每个节点的元素小于等于它的右兄弟(如果有)
P2:对于每个有祖父的节点N,其祖父节点的左孩子小于等于N
P3:对于每个有祖父的节点N,其祖父节点的右孩子大于等于N
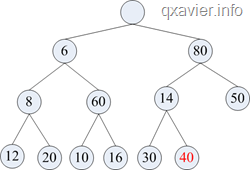
比如下图就是一个双端堆
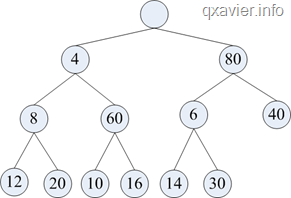
下面我们看看实现
既然是一个满二叉树,那么就可以像堆一样有一个数组来表示,下标为n的节点的左右孩子的下标分别为2×n和2×n+1。
插入操作
现将该元素放在树的最后,看有没有满足性质P1,若违反,交换两节点的内容。再看是否满足上面讲的性质P2或者P3,如果满足,就将元素放在当前位置;若没有:
违反P2,将当前节点与其祖父的左孩子交换,祖父的左孩子变成当前节点;
违反P3,将当前节点与其祖父的右孩子交换,祖父的右孩子变成当前节点。
重复进行判断,直至找到合适的位置。
假设插入2,过程如下图:
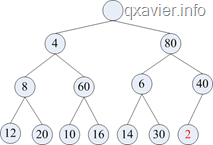 =>
=>
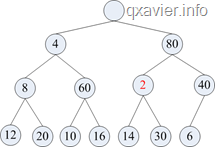 =>
=>
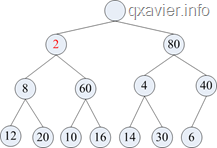
代码如下:
public void insert (T data) throws Exception
{
int curIdx = ++ size;
if ( size >= HEAP_MAX_SIZE )
throw new Exception();
int grandpa;
int parentMin, parentMax; //爷爷的左右孩子
while (true)
{
//是否有更大的左兄弟
if ( (curIdx & 1) == 1 && data.compareTo(heap[curIdx-1]) < 0 )
{
heap[curIdx] = heap[curIdx-1];
-- curIdx;
}
grandpa = curIdx >> 2;
if ( grandpa == 0 )
break;
parentMin = grandpa << 1;
parentMax = parentMin + 1;
if ( heap[parentMin].compareTo(data) > 0 )
{
heap[curIdx] = heap[parentMin];
curIdx = parentMin;
}
else if ( heap[parentMax].compareTo(data) < 0 )
{
heap[curIdx] = heap[parentMax];
curIdx = parentMax;
}
else
break;
}
heap[curIdx] = data;
}删除操作
这里面的删除操作应该是指找到并删除最小(大)元素,找到很容易,最小元素是根的左孩子,最大元素是根的右孩子。但是,删除之后怎么调整以满足双端堆的特性呢?我们以删除最小元素为例,算法如下:
我们将树的最后一个元素暂时放在删除元素的位置,判断两个条件:
是否满足P1,不满足则交换两元素
与其左孩子、以及右兄弟节点的左孩子(如果有的话)比较,是否是最小的,不是则与最小的节点交换。(其左孩子和右兄弟的左孩子是两个次小的节点)
重复以上判断,直至满足这两个条件。
如果删除4的话,过程如下图:
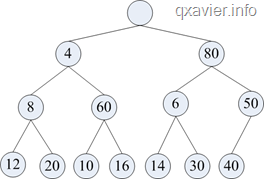 =>
=>
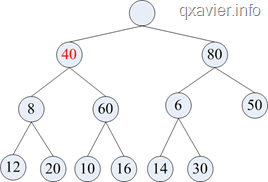 =>
=>
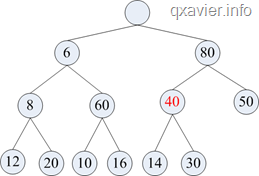 =>
=>
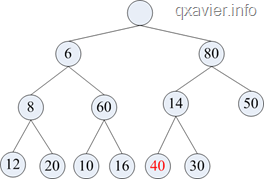 =>
=>
代码如下:
public T deleteMin () throws Exception
{
if ( size < 2 )
throw new Exception();
if ( size == 2 )
return heap[size --];
T tmp;
int minChildIdx;
T data = heap[size --];
int curIdx = 2;
T ret = heap[curIdx];
while ( true )
{
if ( (curIdx & 1) == 0 && curIdx + 1 <= size && data.compareTo(heap[curIdx+1]) > 0 )
{
tmp = heap[curIdx+1];
heap[curIdx+1] = data;
data = tmp;
}
minChildIdx = curIdx << 1;
if ( minChildIdx > size )
break;
if ( ((curIdx + 1) << 1) <= size && heap[minChildIdx].compareTo(heap[(curIdx+1)<<1]) > 0 )
minChildIdx = (curIdx + 1) << 1;
if ( data.compareTo(heap[minChildIdx]) > 0 )
{
heap[curIdx] = heap[minChildIdx];
curIdx = minChildIdx;
}
else
break;
}
heap[curIdx] = data;
return ret;
}所有代码可以在这里看到。